possible related topics algebra, number patterns
Learners could start by estimating the number of dots.
For small numbers of dots in ‘conventional’ arrangements
such as ![]() , most people can subitise
almost instantly with high accuracy. But there are far too many dots here to do
that.
, most people can subitise
almost instantly with high accuracy. But there are far too many dots here to do
that.
One way to work with this beginning is to present the image for a few seconds on the screen and then turn it off. See if learners can recreate it, perhaps in pairs.
To count the dots (without counting them all), learners could consider ways of dividing up the dots into convenient shapes, and this could perhaps be developed algebraically. Arrangements of dots in rows and columns can easily be counted by multiplication.
There is much for learners to investigate. There are 4 dots along the shorter edges and 9 dots along the longer edges. Are these numbers connected? How does the perimeter relate to these numbers? (Will we call the total number of dots around the edge ‘the perimeter’ or will we count the total length round the edge, taking the shortest distance between two dots as one ‘unit’?)
An alternative to cutting up the shape into smaller pieces is to add three equilateral triangles of dots, converting the whole shape into an equilateral triangle, therefore containing a triangle number of dots.

Since there are 15 dots along the base, this is the 15th
triangle number, ![]() .
Since we added three triangles of 6 dots each, we need to subtract 18, giving
102 dots. (Did you think there were more than 100 when you first looked at it?)
.
Since we added three triangles of 6 dots each, we need to subtract 18, giving
102 dots. (Did you think there were more than 100 when you first looked at it?)
Our original hexagon had 9 dots along the longer edges and 4 dots along the shorter edges. In general, with s dots along the shorter edges, there will be 17 – 2s dots along the longer edges. Since 17 – 2s will be odd for all integer s, it means that the longer sides will always possess an odd number of dots.
The perimeter P will be given by
P = 3(s + (17 – 2s)) – 6,
subtracting 6 to account for the dots at the vertices of the hexagon, which are double counted. This simplifies to P = 45 – 3s.
So for s = 4, P = 33.
Generalising the reasoning above, the total number of dots n
will be given by ![]() ,
where
,
where ![]() is the rth triangle number, so
is the rth triangle number, so
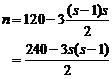
Again, checking when s = 4 gives n = 102.
We can come to various conclusions, such as that at no point will the short and long sides contain an equal number of dots, since the solution to the equation s = 17 – 2s is not an integer.
Other members of the family can be drawn and similar calculations performed.


www.mathematicalbeginnings.com
© Colin Foster 2012, www.foster77.co.uk