Viewpoint

possible related topics estimation, Pythagoras’ theorem, ratio

This photograph was taken from the top of the Willis Tower (formerly the Sears Tower) in Chicago. The Willis Tower is 442 metres high and when it was built it was the tallest building in the world.

Obviously, how far you can see depends on the height of the things you are looking at, as well as your own height: distant mountains are much easier to see than the ground. Clouds and fog impair visibility, but the curvature of the earth also plays a role. Your eyesight may make a difference too!

A diagram such as the one below shows an observer at height h above the surface of a spherical earth of radius r, centred at O, seeing a distance d to the horizon. There are lots of assumptions here, such as the earth being a sphere. (The diagram is considerably exaggerated!)

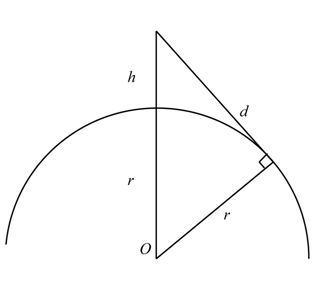
Viewpoint diagram.png

Using Pythagoras’ theorem, , giving .

Since , we can ignore in comparison with , giving an approximate result that

Plugging in a value of r = 6400 km gives , with h and d both in metres.

Learners could consider the advantage of a small increase in height – e.g., standing on tip-toe. How much does that help?

Refraction of light also plays a role, and therefore the distance depends on the temperature of the air. Learners could find out about mirages.

www.mathematicalbeginnings.com